In this week’s blog, we will apply elementary Newtonian
dynamics to model rocket motion and compare a rocket’s burnout velocity and
height on three celestial systems.
To keep our model basic, we will make a few initial
assumptions. Our model will only include
vertical motion, neglect air resistance, and assume constant acceleration due
to gravity. Furthermore, we will assume
that the fuel burn rate will remain constant throughout lift off.
A rocket’s thrust is a direct result of conservation of
momentum. In order for the rocket to
propel itself forward, it must eject mass in the opposite direction. This calculation becomes more complicated as
the rocket’s mass is constantly changing.
Moreover, as gravity is a factor, the external force on the rocket is
not zero.
Given that
where p
is momentum, m is mass, and v is velocity, we can manipulate our conservation
of momentum equation to determine our rocket’s thrust.
Here, u
is the constant burn rate of fuel. Next,
by taking a time derivative of each side, we can determine our thrust as the
time derivative of velocity is acceleration and we know F=ma.
Next, through similar manipulation of our
conservation of momentum equation, we can determine that our rocket’s velocity
is
and by replacing the m value with the appropriate time t equivalence,
Finally, to determine the rocket’s
burnout height, we just need to integrate our velocity equation over the change
in time and mass of flight.
Now, given our rocket’s specs and various
conditions, we can apply these equations to determine, and compare, the burnout
velocity and height of our rocket on Earth, the moon, and Neptune.
Using these values, the burnout velocity
and height on Earth are 2,158.2 m/s and 99,676.6 m, respectively. The burnout velocity and height on the moon
are 3,365.01 m/s and 188,719 m, respectively. The burnout velocity and height on
Neptune are 1,958.99 m/s and 84,977.6 m.





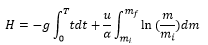

No comments:
Post a Comment