While the motion of a system of coupled oscillators can
be very complex, the system’s eigenfrequencies ω and normal mode motion can be
determined by applying a fairly simple procedure. A system’s eigenfrequencies and normal mode
motion refers to the natural resonant frequencies of the system and the pattern
of motion in which the system undergoes when all parts move with the same
frequency, respectively. To determine
the eigenfrequencies and normal mode motion of a system of coupled oscillators:
- Formulate the lagrangian equations for the system’s kinetic energy T and potential energy U.
- Construct Aij and mij tensors in n x n arrays to describe how the system’s various components are coupled.
- Form and solve the characteristic equation for ω. The characteristic equation is given by
- Determine the eigenvectors of the matrix Aij – ω2mij describing the normal mode motion of the system.
Example 1: Two Pendula
Given a system consisting of two pendula of equal length L and mass m connected by a spring of force constant k, we can determine the eigenfrequencies ω and describe the normal mode motion of the system. Figure 1 illustrates the system.
Figure 1: This figure shows the system of coupled pendula.
Image Credit: Classical Dynamics of Particles and Systems by Thornton and Marion
As our pendula only move about the Θ direction and kinetic energy of an object is described by the
general equation
Similarly, as the potential energy of a
pendulum and a spring are described by the general equations
where g
is gravity and x is the distance from
equilibrium the spring is either stretched or compressed, the total potential
energy of our system is
If we assume our pendula will only
undergo small oscillations, we can simplify our potential energy equation using
the approximations
and
Next, we construct our Aij and mij tensors. The components for each of these tensors is determined by the relations
where qi
and qj represent the
respective generalized coordinates. In
this case, the generalized coordinates are simply Θ1 and Θ2. Thus, our tensors are
and
Next, we form and solve the
characteristic equation for ω. Our
characteristic equation is given by
meaning we must set the determinant of matrix A-ω2m equal to 0 and solve for ω. We find the eigenfrequencies of the system are
Finally, after solving for the
eigenvectors of the system, we determine the normal modes of the system to be
and
This means that our pendula can obtain
constant oscillatory motion two ways: by swinging together at equal velocities
or by swinging exactly opposite eachother, see Figure 2.
Figure 2: This figure illustrates the normal modes of the coupled pendula.
Image Credit: Classical Dynamics of Particles and Systems by Thornton and Marion
Example 2: Three Pendula
Given a similar system to that of example
1 but containing an additional pendulum, we can use the same process to
determine the new system’s eigenfrequencies and normal modes. Below are the respective functions and tensors.









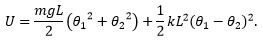











No comments:
Post a Comment